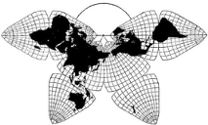
Cahill 1909
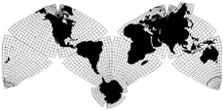
Cahill-Keyes 1975

Cahill 1909
|
Go back to
Gene Keyes home page
Cahill-Keyes 1975 |
|
Notes on Scaling Cahill and Cahill-Keyes Maps
by Gene Keyes Reformatted and updated 2011-06-09 Expanded and revised 2009-03-07; 2009-02-28 Earlier drafts 2007-04-05, 1983-11-16, 1983-11-09, 1983-05-29, 1982-06-27, 1982-06-23 Both diagrams below in this article were originally drawn by Gene Keyes I stumbled into a quagmire attempting to scale
the copies of various Cahill maps I have on hand, and will record these
notes before I forget how I resolved the problem. [Here referring mainly
to Truncated Octahedron 9-sided octants, or nonagons: not the complete triangles
of the Gnomonic or Conformal variants.]
It turns out that Cahill-Keyes maps bear a single nominal scale, whereas Cahill maps can have up to five scales (including two nominal), depending on the criteria used. [See appendix 1 below.] By design, the Cahill-Keyes octant perimeter is approximately in scale to its nominal globe: the equator and the two outer meridians of the octant are each 1/4 of a great circle on a 100.425% perfect metric sphere. (More details here.) Hence on Cahill-Keyes, the equatorial scale and the nominal scale are the same. However, the Cahill octant only has one-way symmetry: not three-way symmetry like mine. Cahill’s nonagon has shorter meridianal mid-segments than equatorial, whereas mine are all equal. Likewise, the end-segments on Cahill octants are unequal, north / south / equatorial. For a given Cahill octant and a Cahill-Keyes octant, each with a 90 mm altitude, Cahill’s has an equator of 93 mm, v. mine of 100. (e.g., p. 202, J.Assoc.Eng.Soc.) Note, however, that the optimal [or optimal / nominal] basis of comparison is the “Scaffold” altitude of the circumscribing equilateral triangle, and hence these are not otherwise comparable octants, Cahill’s having a scaffold altitude of ca. 104 mm v. mine of 100 mm (i.e., 10,000 km). Therefore, my chosen basis of comparison is the span between the outer vertical sides of 4 octants in an arch, or 8 octants in an “M”, representing my [Coherent World Map System] spans of 20,000 or 40,000 km respectively, or 2 or 4 lengths of the scaffold triangle altitude. I will call this a Comparison Scale (which may vary a little from other ways of interpreting a given map’s scale). 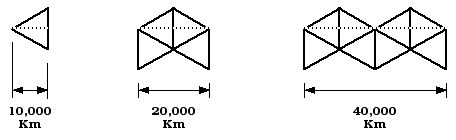
Thus, the spread-out M-profile represents the circumference
of the earth, 40,000 kilometers: the world unfurled. (Maximum shrinkage
/ distortion in a Cahill-Keyes map ocurs along the central meridian of each
octant, but in assemblies of four or eight octants, the nominal relation
of width to earth-circumference is preserved.) See appendix
2 below.
The Comparison Scale occurs in two usages: (1) An enlarged or reduced version to accord with a specified scale, often 1/200 M, so that any two or more maps may be compared regarding their distortion, graticule, etc. (2) A recalculated original scale of the map, based on its 4-octant span as divided by 20,000 km. (Since the Comparison Scale happens to be an equatorial scale as well, other non-Cahill, non-Butterfly world maps can be likewise adjusted by setting their equator within a 200 mm frame.) Given that the M shape is not the prevailing mode of Cahillian maps, it is sufficient to use the 4-octant subset, for calculating the map’s existing scale, and/or the percent increase or decrease needed to put the map into a size where all examples can be compared: say, 1/200 M, where the 4-octant length is 100 mm and the full 8-octant length is 200 mm). Thus, with 100 mm as a numerator, we can use a calculator with a 1/x button to get the full 200 mm, 1/200 M conversion percentage, by using the length of the 4-octant span, representing half the entire map. For instance, Dahlberg’s Cahill illustration is 48 mm across a 4-octant span. Entering 48 mm in a calculator with a 1/x button produces a 208.3% enlargement factor, resulting in the Comparison Scale of 1/200 M. Whereas the map’s unchanged original scale — as derived from the Comparison Scale — is 1/416 M: 2 x 48 = 96 mm / 40,000 km [earth circumference] = then 1/x = 1/416.6 M. [Leaving aside zeroes in calculator entry and readout.] Comparison calculation: take a Cahill-Keyes 8-octant span of 200 mm, divided by 40,000 km = 0.005, then 1/x = 200 [1/200 M] Note that the same results obtain when using the 4-octant span, representing half the earth’s circumference: thus, Dahlberg’s Cahill, 48 mm / 20,000 = 0.0024, then 1/x = 1/416.6 M. Cahill-Keyes, 100 mm / 20,000 = 0.005, then 1/x = 1/200 M. For a given 1/100 M map, a Cahill version by the other
four scaling criteria (below) might be 15% larger than mine at the same
scale: in principle, mine shrink in vis-à-vis a scaffold
triangle, whereas his stretch out, especially his Conformal and Gnomonic
versions.
The Keyes-Comparison Scale posits that the width of a rectangle enclosing an entire world map [M-shape or comparable] at 1/100 M be 400 mm, representing a metric Earth circumference of 40,000 km. (Or 200 mm for a 1/200 M map; etc.) Likewise, a square enclosing a four-octant arch, representing half the earth and half a metric earth circumference of 20,000 km, is deemed to be 200 mm if 1/100 M, or 100 mm if 1/200 M, etc. (Because the Butterfly shape is not as wide as the M-shape, we must use the half-a-map, four-octant arch, to align with a 20,000 km measurement.) With size-adjusting software, a map image can easily be fitted into such a rectangle, and imputed with the given Comparison Scale, even if its scale might vary somewhat by other ways of measuring.
_________________________________
^ APPENDIX
1:
Five different scales of a Cahill map with truncated octants (Equal-Area), depending on criteria:
1) Main Scale would be according to preponderant lengths per
10° of latitude, divided into 11.1. (Say, at 40-50° N or S, at
22.5° E or W from outer meridian.)
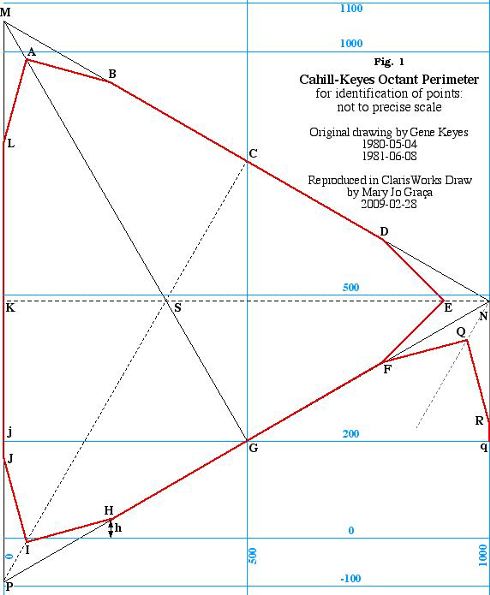
2) Natural Scale would be per Map Scale Indicator (a special ruler from Memorial University of Newfoundland Dept. of Geography), based on 1 statute mile, 1 kilometer, 1,000 feet, or 1° of latitude. 3) Nominal Scale 1 would be length of 1/3 of octant perimeter divided into 100. (Equatorial.) 4) Nominal Scale 2 would be length of the (truncated) altitude divided into 100. 5) Comparison Scale (or Keyes-Comparison Scale) as detailed herein: the span between the outer vertical sides of 4 octants in an arch, whereby the altitudes of the circumscribing triangle are deemed to be 100 mm for a standard scale of 1/100 M, and the width of the arch is adjusted to 200 mm. (Or a 50 mm altitude for 1/200 M; etc.) While not the right place to discuss minutiae
of the Cahill-Keyes design, this diagram indicates the relation of its nonagon
to a circumscribing "scaffold" triangle. Each main side has three segments
constructed to jointly equal 1,000 km. (Further elaborated here.)
|