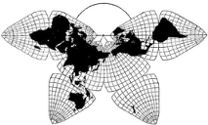
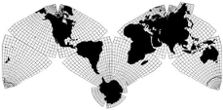
Cahill 1909
| Go to complete linklist of Cahill-Keyes map development | |
| Go to Gene Keyes home page | |
 |
 |
|
Cahill 1909
|
Cahill-Keyes 1975 |
|
Cahill-Keyes World Map Wall Poster
Duncan Webb version, 2014 2020-07-30: SORRY, OUT OF PRINT
|
To view this already reduced image at half-size, click in it once. To restore full size, click in it twice.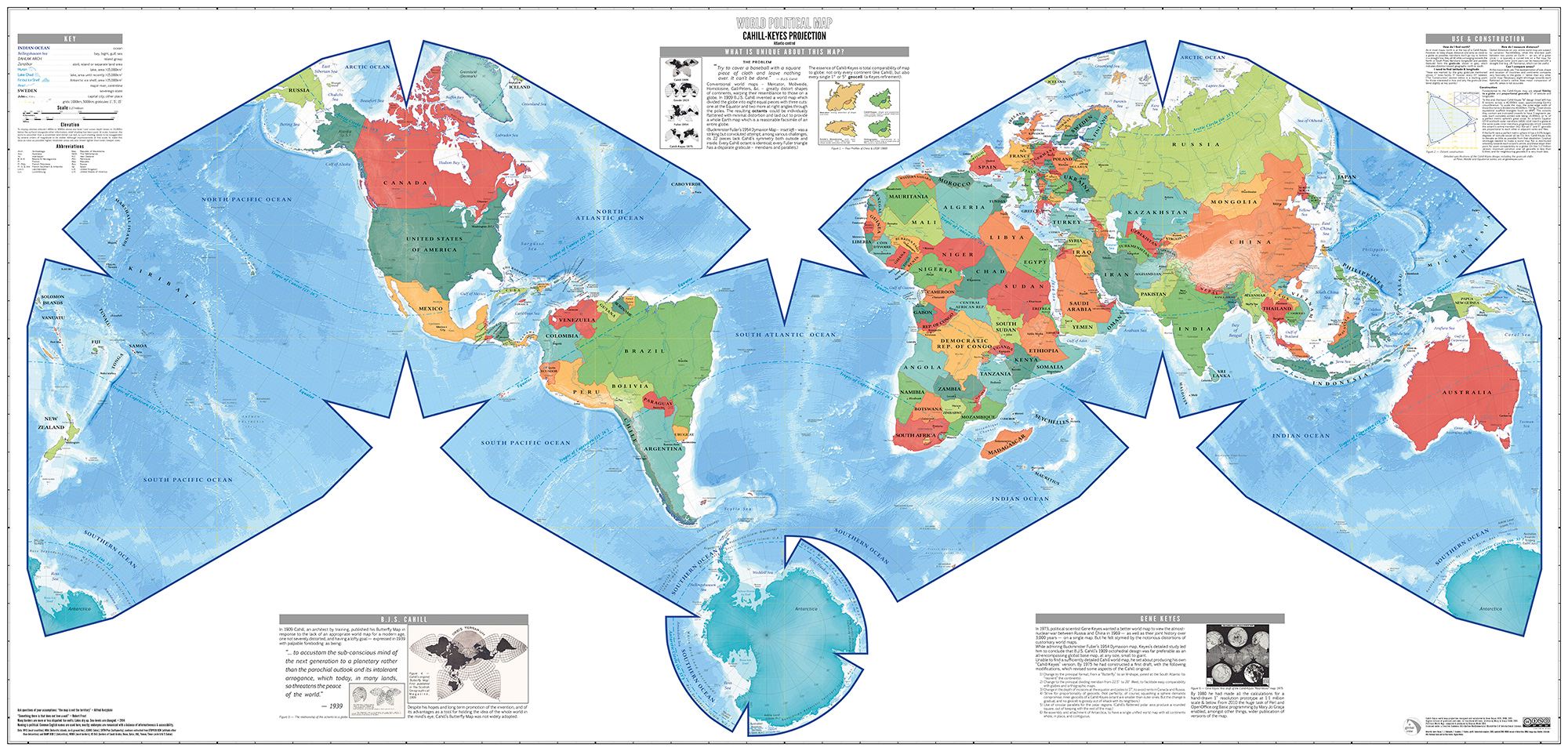 Designed and calculated by Gene Keyes Programmed in Perl and Apache OpenOffice Draw by Mary Jo Graça This version compiled and produced by Duncan Webb, 2014 |
|
Duncan Webb's Commentary and YouTube
Beautifully printed; extraordinary details. Watch the video tour for more.
What is unique about this map?
Being able to think clearly and accurately about our planet-wide interconnectedness has never been more important. A Cahill-Keyes world map makes that easier. Other world maps have their own attractions, but are well-known for their distortions. Cahill-Keyes is a great map to help you understand those distortions and avoid making misleading assumptions about the world as a whole.
Or watch directly on YouTube, choosing the HD option from the cog at bottom right, for better resolution. Continuing Cahill's goal:
... to accustom the sub-conscious mind of the next generation to a planetary rather than the parochial outlook and its intolerant arrogance, which today, in many lands, so threatens the peace of the world. —1939 From the family of B.J.S. Cahill:
This map has received kind support from the family of B.J.S. Cahill:
As descendents of the inventor of the "Butterfly Map" we think it is wonderful that Gene Keyes has worked so hard to bring it to life in such a dramatic new version. The Cahill-Keyes map represents a significant milestone in cartography and we celebrate its availability as a poster to cartographers, map enthusiasts and the world at large. Specifications:
The dimensions of this 1:27 million World Political Wall Map are 1,560 mm x 750 mm [61" x 29"]. The map is lithographically printed at high resolution. The paper is poster weight (170gsm) and will benefit from mounting on Gatorboard or similar.
Cahill-Keyes in the media:
The New York Times
Wired.com (Erratum: projection is not "octal gradient", but "Cahill-Keyes Octant Graticule") Find out more:
For details of the construction of this projection, and its creators, see Gene Keyes and B.J.S. Cahill.
|