Since 1917 Mr. Fuller has been evolving
his Airocean World Map and new projection method — searching
for the best way of seeing the traffic pattern of the Air World's
"Town Plan." In 1927 he made his first map "sketch" of the "World
Town Plan" with full forecast and illustrated documentation of
the present day — 1954 — world airline routes in his book 4.D, privately
published in Chicago. In 1938 he published an improved map "sketch"
of the Airocean World as the end-papers of his book
Nine Chains
to the Moon, Lippincott, publishers. In 1940,
Fortune
Magazine published his world map "sketch" in a presentation of Fuller's
"World Energy Map." In March 1943.
Life Magazine published
"The Dymaxion World," Fuller's first true disclosure of his mathematical
projection invention. The
Life edition portrayed accurately
but awkwardly the Airocean World — for the sinuses intruded several
of the continental masses. In the spring of 1944.
Neptune Magazine
published an improved orientation by Fuller of his true mathematical
transformation. This avoided sinuses intruding the continents and
provided a world map greatly improved over the
Life edition.
Unfortunately, however, it frustrated inspection of over-the-Arctic
flight, for a sinus intruded the Arctic Ocean.
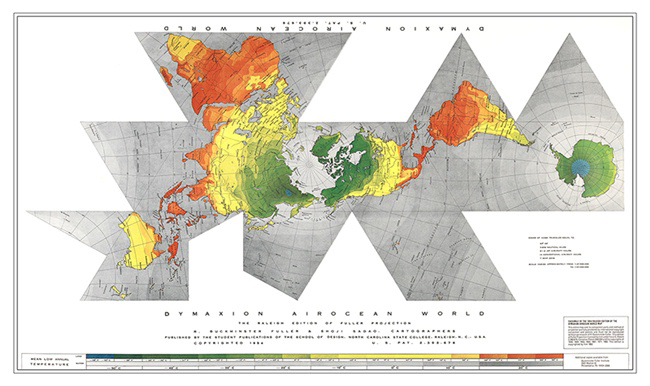
In the present 1954
Raleigh Edition
of Fuller's true mathematical projection presented herewith
and published by the Student Publications of the School of Design,
North Carolina State College, he has reoriented the sinuses in such
a manner that all the previous objections have been overcome.
Due to its inherent advantages in respect
to astronomical observation. aerial mosaicing and comprehensive
world triangulation by great circle grid — while containing
within its continentally unsinused surface all the major, shortest
air routes between the most people — the
Raleigh Edition
of the Fuller Projection comprises a world-around Airocean strip
map of approximately invisible dimensional distortion and as such
will probably in due course be commonly recognized as the best single
world map of the Air Age. Because it is a mathematical revolution
and mathematics are fundamental, its broad acceptance will be fundamentally
slow.
The
Dymaxion Airocean World Map
and its projective transformation strategy was glimpse.conceived
in 1917, but required what has turned out to be over a third
of a century of mathematical exploration in what Mr. Fuller named
"Energetic and Synergetic Geometry," to bring
it at last to its present condition of: "satisfactory." It is satisfactory
because it is the least distorted means of studying at one glance
the total synergetic significance of Airocean economics and the
alternate strategies for integrating all phases and states of energy
behavior resources toward the highest operative advantage of all world
people.
To confound those who "know all about geography"
— from a Mercator projection — and who say that we go from
the U.S.A. west to the Orient and east to Europe, Mr. Fuller
has discovered the "Dymaxion Equator." The Dymaxion Equator is
a great circle running approximately due east and west through a
point on the Pacific Coast of the US.A. about two hundred miles
north of San Francisco. The Dymaxion Great Circle through this point
has "50 - 50" as its North Pole, i.e., 50 degrees East longitude by
50 degrees North latitude, and 130 degrees West longitude by 50 degrees
South latitude as its South Pole. This Dymaxion Equator runs from Cape
Canaveral, Florida, through the U.S.A. to Cape Mendocina, California,
then due west through a point 130 degrees West longitude by 40 degrees
North latitude. north of Midway Island (far north of Hawaii), north
of Wake Island, passing over the seventy-five mile northern neck of the
island of New Guinea, thence through the Malay Straights north of Australia,
thence across the Indian Ocean running due west through a point 50
degrees East longitude by 40 degrees South latitude, and thence just
south of Cape Hope, South Africa, and thence through the South Atlantic
just north of Brazil and thence returning to the U.S.A. at Cape Canaveral,
Florida, having gone completely around the world on one great circle
course without touching any other continent than North America and having
passed over twenty-one thousand statute miles of open ocean waters. In
the Southern Hemisphere of the Dymaxion Equator lie only "Greater Texas,"
Central and South America, Australia and Antarctica. In the Northern Dymaxion
Hemisphere dwell 93% of the human family.
The Fuller Comprehensive World Projection
— or Transformation — is contained entirely within a plurality
of great-circle.bounded triangles — or quadrangles — of constant,
uniform modular subdivision whose identical length edges — shown
as steel bands in the illustrations on this page — permit their
hinging into flat mosaic-tiled continuities at the planar phase
ot the transformation and thereby permit a variety of hinged-open complete
flat world mosaics.
As in skinning an animal, a fruit. or a vegetable
to provide a flat skin stretch-out, the development of a flat map
of the complete world involves arbitrary piercing of the world ball's
surface map-skin, thereby making one or more holes or gashes from
which to start the stretching-out and peeling-off process of the
skin until it is liftable from off its ball center. After the data
has been further stretched it may be laid out as one or more flat map
sections. If the skinning is accomplished in separate peelings and
those sections have curved peripheries they may be associated only
tangentially, e.g., as "gears" or "fans," which destroys the chance
of forming a continuous one-surface comprehensive world map.
To provide a continuous one-surface world map —
while peeling off the sections of the globe — the transformation
must be such that the pieces have straight and matching edges when
peeled off and flattened out.
Unlike any of those of its cartographic predecessors
which present the whole spherical world surface data within
a unit flat surface map — a few cases of which are shown on this
page — the Fuller Projection maintains a uniformly modulated and
constant length great circle boundary scale in closed — 360 degree
— equilateral periphery controls.
The Fuller Projection operates in a series of transformation
stages. It first subdivides the total world surface into a plurality
of great circle bound polygonal zones. Next it transfers the data
froni the sphere's surface in separate mosaic "tiles" corresponding
to each of the great circle bound polygonal zones of step one. While
migrating as a zonal mosaic tile, each tile (independently) transforms
internally from compound curvature to flat surface by methods shown
on this page and later described. Each tile transforms entirely
within the respective polygonally closed uniform symmetrical containers,
allowing none of the data to spill outwardly in perverse distortion.
When all of the tiles have transformed independently
from spherical to planar, their straight polygonal edges — unaltered
in length during the transformed-in-transit migration — permit re-association
in a variety of continuous data mosaics.
The Fuller Projection has the relationship to all
other known projection methods that a mechanically fillable and
sealable set of flasks bear to hair combs, hair pins, fish bones,
and star spurs, as instruments of liquid transfer.
The Fuller Projection not only contains its surface
data increments within uniform and linearly unaltered closed great
circle arc polygonal peripheries — all the way from its spherical
to its planar positions — but also uniquely
concentrates
all of its spherical angle excess. It concentrates the excess into 360
degree symmetry within equilateral polygons. This means that the compound
curvature subsides by symmetrical internal
concentric contraction
into a flattened condition entirely within its neither elongating
nor shortening peripheral integrity. The internal subsidence of
the Fuller Projection is in contrast to all predecessor
projective methods for showing the whole world within one unitary
surface. All the predecessors disperse spherical excess by outward
"fanning"-i.e., by
stretching out to flattened condition.
Spherical excess is the amount of angle by which
the three internal angles of spherical triangles exceed the constant
internal angular sum of 180 degrees — which characterizes all
planar triangles. The internal angles of spherical triangles always
add to more than 180 degrees and the larger the spherical .triangles
the greater the "excess." Convince yourself of this infraction of
your planar thinking by drawing a meridian of longitude which is a
great circle from the North Pole to the earth's equator, which is
also a great circle. Meridians and the equator always intersect each
other at 90 degrees. Draw a line along the equator a quarter way around
the world, which is 90 degrees. Then draw a line returning by meridian
90 degrees to the North Pole. You will have completed a spherical triangle
whose three angles are each 90 degrees and add to 270 degrees, or 90
degrees "spherical excess."
Because the area of a circle of radius "2" is approximately
four times the area of a circle of radius "1," when the dimensional
variables of a projected surface are outwardly distributed, the
proportion of total map area that is in relatively greatest distortion
exceeds by the ratio of three to one the relatively least distorted
areas. When — as in the Fuller Transformation — the spherical surface
subsides inwardly by symmetrical contraction, then the proportion
of the map which is in relatively greatest dimensional distortion is
less by a ratio of one to three than its relatively undistorted area.
How the Fuller Projection transfers the spherical
data to the planar — employing only great circle coordinates while
all other projections employ a progressively complex admixture of
great circle and lesser circle coordinates — is shown in the two columns
to the right.
[Below. —
GK]
At outset of the Fuller Transformation — from spherical
to planar condition — radii of the sphere of reference which penetrate
perpendicularly each spherical surface coordinate point of the
comprehensive great circle grid, separate from one another at their
respective internal ends — at the center of the sphere — and each
and all remain constantly perpendicular to the transforming, internally
shrinking surfaces
throughout the transformation, and their original
uniform lengths also continue as "constant" throughout the transformation.
Because of the constant perpendicularity of the
Fuller Projection's radii to the transforming surface, the Fuller
Projection greatly simplifies celestial calculations. All astronomical
phenomena always occurs in outward perpendicularity — zenith — to
the Fuller Projection's internal spherical coordinates. On transformation
to planar grids the astronomical data always remains in identical
perpendicular zenith to the corresponding coordinate positions in
the planar phase of the Fuller Transformation.
Because of this property, the Fuller Transformation
would be more suitable than any other projection for a comprehensive
planar mosaic of a total covering-set of world-around aerial photographs.
Aerial photographs are always taken from zenith positions and at
constant altitude, or radius distance from the earth's spherical
surface.
The Fuller Projection, consisting of great circle
bounded triangles of any angular magnitude, can transform the
comprehensive geographical data of the world from spherical to planar
by employment of either the spherical tetrahedron, spherical cube,
spherical octahedron, or the spherical cubo-octahedron and its alternate,
the icosahedron, or any development of these four respectively. It
is a discovery of Energetic Geometry that there are no other spherical
triangular grid bases other than the above.
However, it is a matter of Dymaxion cartographic
strategy that: — the greater the number of great circle polygonal
zones employed in the transformation the less the spherical excess
to be subsidingly concentrated within each zone surface respectively,
and therefore the less the residual distortion distributed to each
of the planar mosaic aspects of the whole world's reassembled surface
when arrayed in one continuous fiat "skin."
The Fuller Projection is patented and represents
the only method by which the whole world data can be transferred
from the spherical to the planar —
within an all great circle
grid, triangularly, quadrangularly, multi polygonally, or all
two or three together. Because of a hemisphere's polar symmetry
to its opposite polar hemisphere the total inventory of great circle
grid triangles in the comprehensive world grid is always even in number,
therefore adjacent triangles may always be associated in total or partial
quadrangular pattern-phases without increase in vertex count.
Because automatically guided long distance fiight
of aircraft or missiles most profitably follows the great circle
— or shortest spherical distance courses — the guiding of aircraft
or missiles can only be operated accurately on a world-around scale
when referenced to a world-around triangular great circle grid survey.
The Fuller Transformation will in due course become the appropriate
cartographic device for plotting and planning such world encircling
aeronautics.
It is no secret to the Soviets and it is well known
in cartographic circles that because both the North and South American
continents have been triangularly surveyed and gridded and the triangulation
was carried across to Africa and thence into Europe and the Near
East, India, and Australia, to satisfy the needs of World War Two,
and the triangulation published, that the Soviets now know
exactly
where the U.S.A. and all its strategic resources are located, and that
because the triangulation has never been extended into the Soviet
Union and much of Soviet dominated Asia, we do not know with mathematical
accuracy where most of the Soviet's resources are. We do not know within
a vital margin of several precise miles.
But, the surveyed triangulation around the Soviet
Union and Soviet dominated Asia ever closes in. Some day when
the basic causes of lethal threat have evoluted to non-critical
magnitude — the direction in which they now fortunately accelerate
— through swiftly multiplying industrialization — then the inventory
of controlled missile programming will be converted into controlled
cargo and passenger routings to any point half way around the world
in one hour.
It is to be noted that because the geometric constants
or controls of all conventional projections are predicated upon
a three dimensional coordinate system — comprised of an admixture
of great circles with a variety of non-uniform lesser circles — that
the
constants which provide the original reference controls
inherently are broken open and their
finite quality converted
to
infinite — in respect to some part of their transformation
data.
It is also to be noted that the internal earth
lines formed in the intersection of all three dimensional coordinate
planes of all predecessor world projection methods represents a
hodge-podge of lengths and angles-of-incidence to the earth's external
surface. When the surfaces are stripped of the earth and arranged in
projected planar condition; these lines and angles look like a
runover porcupine.
The lack of coincidence of three. dimensional coordinate-radials
with the spherical radii and non-uniform radial length of the
three-dimensional coordinate and non-perpendicular incidence of
three-dimensional radials upon the spherical surfaces, has caused
a heterogeneity of angles and lengths in respect to all conventional
projections, which in turn has added frustration and entirely unnecessary
awkwardness and complexity to the trigonometric problems of navigational
science.
This unnecessary awkwardness of three-dimensionality
has also promoted the calculus in "blind" calculations, where
visual transformations might otherwise have accrued to a simplified
multidimensional spherical trigonometry (which latter is rarely
taught in school or college). The much simplified spherical trigonometry,
plus a permeative topology, plus quanta and wave mechanics, plus
thermodynamics, plus chemical structures, integrate as Energetic
and Synergetic Geometry, which sum totally is no more difficuit than
is the visible reading of this map, which is visible Energetic and
Synergetic Geometry — nor reading the Energetic-Synergetic Geometry
illustrations of its transformation processes.
The Fuller Projection great circle grid employed
in the
Raleigh Edition of the
Dymaxion Airocean
World is that of the spherical icosahedron, chosen because the
latter has the largest number of identical and symmetrical spherical
triangles, and therefore the least "spherical excess" of all the
possible symmetrical triangular great circle bound mathematical
cases.
The spherical icosahedron was also chosen because
its controlling arc boundary of 63 degrees 26 minutes 05.816
. . . . . seconds was just adequate to the triangular spanning
of the maximum continental aspects encountered in the unpeeling
of the earth's data — within twenty symmetrical great circle bound
control triangles — spanning those continents in such a manner that
all twelve vertices of the spherical icosahedron grid lay in the open
waters of the continuous world ocean. As a result, this peeled strip
map contains all the world's continental contours respectively. The
Raleigh Edition of the Fuller Projection presents the whole
data in such a way that there is no visible discrepancy in the relative
area sizes and no displeasing distortions of the shapes.
The map may be cut out around its periphery and
bent on its main triangular edges and the exterior edges brought
together — closing all exterior sinuses — thus making a continuous
or finite surface and constituting a planar faceted icosahedron
transformed from the spherical icosahedron.
When the surface is thus closed — proving itself
to be afinite continuity — and the resulting icosahedron is compared
to a globe of the world, the relative shapes and area sizes will
be found to be entirely faithful to the spherical globe's relative
sizes and shapes.
Because the
Raleigh Edition of the
Dymaxion
Airocean World gives the continental stretch-out over the North
Pole without continental contour sinuses and also avoids sinuses
in the Arctic area, it will probably be as appropriate to future
air voyaging as was the Mercator map appropriate to the square rigged
east-west sailings with the Trade Winds — closely paralleling the Equator,
around which the Mercator projection was least distorted.
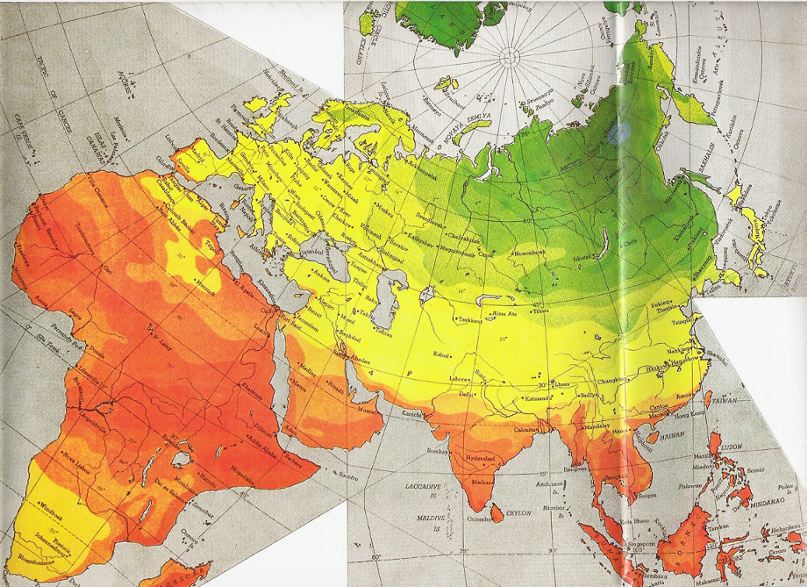
Typical of the comprehensive information that may
be quickly witnessed by the
Raleigh Edition, is that the
jet stream of the northern hemisphere whirls its 300-400 miles-per-hour
course approximately over the green-to-blue area of the central
target-like pattern, giving the Soviets on Cape Deshneva in northeastern-most
Siberia a continuous jet-assist catapulting in a three hour flight
to Chicago, while our own Greenland or Labrador springboards, though
jet stream serviced, are not assisted in the correct direction to reach
any of the Soviet "Chicagos."
This statement is no "comfort" to the Soviets who
already know this and have been too long exceedingly comfortable
in this respect due to our own prevailing public ignorance of dynamic
Airocean geography, we being as yet blinded by old-plate-stocked Mercator
projection vendors, and by the historical east-west orientation
inertia. It is hoped that a new north-south dynamic world orientation
will be aided by the
Dymaxion Airocean World.
The map used by the United Nations on their official
symbol, though disadvantaged by an awkward, old-fashioned projection,
was a vigorous step in the direction of corrective orientation.
Our western "ramparts" of Hawaii may be seen on
the Fuller Projection,
Raleigh Edition, to be only
a little less remote to the "show" than is Robinson Crusoe's Island.
All the old-world-conceived pre-Airocean strategies of controlling
the waterfronts from "down under,"— which took us into Europe's "soft
belly" via Africa, and into Japan via Australia in World War Two, instead
of throwing our science into winning an over-the-North-Pole competence,
— as yet shows up in our present focus on Formosa which, as can be seen
on the Dymaxion Airocean World Map, is looking in the opposite direction
from that in which lie both our potential destruction and our potentials
of salvation, and most importantly of all, our potentials of greatest
world service and competence which alone through demonstration of responsibility,
adequate knowledge and technology can accelerate our preoccupation
in directions that could eliminate the basic cause of utter disaster.