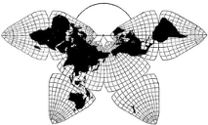
Cahill 1909
|
Go back to
Gene Keyes home page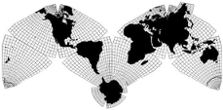
Cahill-Keyes 1975 |
Notes on Re-designing
B.J.S. Cahill's Butterfly World Map
Gene Keyes
2009-12-30
(see Afterword at end)
2009-12-30
(see Afterword at end)
The creation of a master plan of the world is a matter of design first and foremost, the design of a frame within which intensive mathematical details shall be afterwards subordinated— B.J.S. Cahill, 1928
Since 1975 I have been a strong advocate of B.J.S.
Cahill's octahedral "Butterfly" world map. Prior to that I had
intended to adopt Buckminster Fuller's icosahedral Dymaxion design
for my "Coherent World Map
System", but closer examination showed too many underlying
flaws (detailed critique
here), as compared to Cahill, whose invention was to prove a
far better choice.
While I would have preferred an "off-the-shelf" Cahill map to incorporate into my System, in 1975 I was unable to locate large-scale reproductions, drawings, or computations, so I set about drawing my own Cahill from scratch. Later, I did find bigger originals in the Cahill archives in 1982 and 1983, but by then I had designed, and now prefer, my "Cahill-Keyes" version of the octahedral.
Having selected Cahill's approach, I determined that a number of revisions were desirable, to optimize the very large scale Megamap and submaps I was working toward. Those require a reasonably proportionate set of geocells throughout, to closely match my proposed cognate globes which would likewise have at least a 5° graticule, and preferably 1°.
Much trial and error, plus lengthy notebooks and math tables were entailed. Posting them here awaits another day. Meanwhile, this page briefly explains my major revisions to the Cahill design. They are:
To elaborate:
1) Change principal format to an M-shape, joined at south Atlantic.
While I would have preferred an "off-the-shelf" Cahill map to incorporate into my System, in 1975 I was unable to locate large-scale reproductions, drawings, or computations, so I set about drawing my own Cahill from scratch. Later, I did find bigger originals in the Cahill archives in 1982 and 1983, but by then I had designed, and now prefer, my "Cahill-Keyes" version of the octahedral.
Having selected Cahill's approach, I determined that a number of revisions were desirable, to optimize the very large scale Megamap and submaps I was working toward. Those require a reasonably proportionate set of geocells throughout, to closely match my proposed cognate globes which would likewise have at least a 5° graticule, and preferably 1°.
Much trial and error, plus lengthy notebooks and math tables were entailed. Posting them here awaits another day. Meanwhile, this page briefly explains my major revisions to the Cahill design. They are:
1) Change principal format to an M-shape, joined at south Atlantic.
2) Change principal dividing meridian to 20° W.
3) Change incisions at equator and poles to 17°.
4) Strive for proportionality of geocells.
5) Use circular parallels for the polar regions.
6) Re-assemble and attach Antarctica.
To elaborate:
1) Change principal format to an M-shape, joined at south Atlantic.
Most published versions of Cahill's world map were in its metaphorical "Butterfly" pattern, with raised wings at either end, joined at the north Atlantic or north Pacific (or, regrettably, joined at both oceans, with Eurasia split.) My initial hesitation to go with the Cahill Butterfly was that its place names, and country orientation, could not be sufficiently horizontal for an all-encompassing, all-purpose Master Map.
My eureka moment came on March 9, 1975 when I reconfigured the Butterfly to an "M" joined at the South Atlantic. (Before I saw that Cahill too had pictured that as a possibility — though never his definitive one.) This gave me a profile which essentially echoes the prevailing arrangement of commonplace maps, with New World on the left, and Old World on the right, north up, south down. Nothing sacrosanct about any of that; only customary like QWERTY, for all its faults.
But this also gives me a "Master Map" profile in which every sub-square or rectangle is approximately "right side up", at least by habitual usage (notwithstanding other orientations out there, including Fuller's). And in which all place names won't have to be read sideways or upside down. (Sub-sheets of Cahill-Keyes can have meridians slanting up to 60 degrees, but that's tolerable. See Megamap prototype photos here.)
In my 1973 MA thesis, my quest was for a single Master World Map from which all other submaps at any scale could be derived (as cutouts: literally, or in principle). And, conversely, to assemble that same Master World Map, or a Megamap, from squares that are page-size or larger.
Of course, there is no "right side up" for a map, but as a practical matter one wants to be able to print all the place names in the same left-right direction. This does not rule out other patterns for other purposes, including the classic Butterfly in its north Pacific or north Atlantic configuration; or a south Pacific M.
Once I hit on the M-profile as the standard, then everything fell into place. For instance, the M-profile gives me a horizontal frame width depicting 40,000 km, the circumference of the Earth. This ties in to my design feature of showing the entire kilometer-span of any panel of the Coherent World Map System, including the Master Map profile itself, in squares of specified length. The Butterfly mode is not as wide, and cannot, therefore, indicate the spread-out circumference of 40,000 km. (For a diagram, see "Notes on Scaling Cahill and Cahill-Keyes Maps".)
2) Change principal dividing meridian to 20° W.
3) Change incision length at equator and poles to 17°.Cahill had chosen 22.5° W to be one of the two dividing meridians to quarter the globe, plus the equator, for eight pieces.
When I began my re-make of the Cahill, at first I followed his 22.5° starting point, but soon found it to be ungainly. It was:
• much harder to draft;
• resulted in far too many unsightly and asymmetrical half-degree geocells;
• spoiled the smooth comparability of the world map to a counterpart globe or orthographic (globe-like) map, due to the non-alignment of all the edges to a rational meridian.
Therefore, I moved the line 2.5° eastward, without affecting the map's ability to show unbroken continents, but greatly improving its match to a globe, and overall appearance. (Independently of me in 1996, Steve Waterman published a Cahill-type Butterfly world map, which likewise relocated the dividing meridian to 20° W.)
I constantly emphasize the need for world maps and their spinoffs to have at least a five degree, or preferably one degree graticule. Because of that 2.5° mis-step, Cahill's early maps have a very misleading geocell net of 7.5°, which hide their half-degree asymmetries (e.g., the one at the top of this page, next to mine of 5°). It was not until 1936 that Cahill drafted a complete [Equal-area] map at 5°, the "C" version cited below: unfortunately, never published (except for a small partial diagram, mixed with others: here, p. 103). For the complete hitherto unpublished 5° layout, see entire map at this link, Fig. 9.2.1.
To minimize interrupting the continents, I settled upon an incision length of 17° from the poles, because, unlike Cahill's 22.5°, that does not gouge the northern Asian mainland at the Yamal peninsula, nor the northern Canadian mainland, nor the large Victoria Island in the Canadian Arctic. (Waterman went with 18°.)
Cahill, seeing 22.5° as one-quarter of pole-to-equator distance, had also decided to apply that figure to the amount of incision from the poles, and equator. I found his fancy for 22.5° to be an over-reach for symmetry. (At the same time, Cahill's octants only have one-way symmetry, just from the equatorial base and polar vertex, whereas mine have three-way rotational symmetry, vis a vis all three main vertexes and all three main sides.)
Below are illustrations of Russia's Yamal Peninsula.
Fig. 1. Satellite view
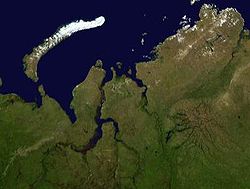
Source: Wikipedia, GydaTajmyrJamal.jpg
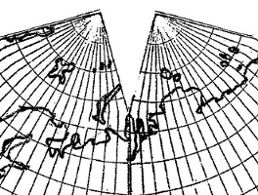
Fig. 2. Cahill, 1936, unpublished draft of "C" version:
its 22.5° cut pierces deep into the Russian mainland.
(Notice, incidentally, that the polar geocell height from 90-85° is twice that of those from 85° downward; further discussed in point 4 below.)
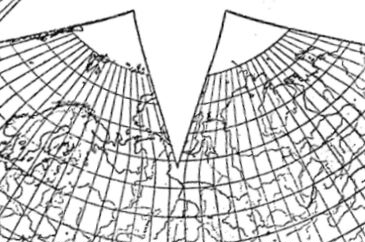
Source: Cahill archives, Bancroft Library, item 57.
Xeroxed, spliced, and scanned by GK
entire map at this link, Fig. 9.2.1
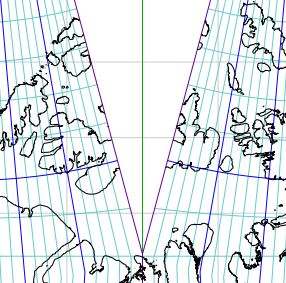
Fig. 3. Cahill-Keyes, 1975, unpublished draft:
its 17° cut does not enter Russian mainland.
Source: Gene Keyes
Fig. 4. Waterman, 1996:
its 18° cut splits into Yamal Peninsula somewhat.
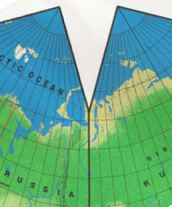
Source: reduced scan of personal copy;
or see http://www.odt.org/Index.htm
or CAHILL_GALLERY/1996-Waterman-ODT.html
Also, whether in Cahill's map or my revision, Russia's far east Kamchatka peninsula, Greenland, Iceland, and the Canadian Arctic Melville Island are unavoidably nicked or split. But these can each be restored by an annex piece, without suffering a permanent "V" shaped indent, as in Cahill's Yamal. The Antarctica segments likewise can be reunited, and joined to one of the octants, preferably South America. There are still a pair of small V-splits in my reassembled Antarctica, which will have to remain as minor blemishes.
Update 2012-02-08: Incidentally (and coincidentally), Melville Island is now politically divided, as in the C-K map split, at the same 110° W. According to Wikipedia,
It is the 33rd largest island in the world and Canada's eighth largest island. Melville Island is shared by the Northwest Territories, which is responsible for the western half of the island, and Nunavut, which is responsible for the eastern half. The border runs along the 110th meridian west. [Nunavut is a new Canadian federal territory formed in 1999. — gk]
~ ~ ~
Source: Screenshot from 2011 digital version of
Cahill Keyes Multi-scale Megamap, Beta-1: download pdf from. http://www.genekeyes.com/MEGAMAP-BETA-1/Megamap-Beta-1.html
This next one is paramount:
5) Use circular parallels for the polar regions.When I first examined a magnified version of a Cahill Butterfly, I noticed that adjoining rows of geocells could be quite disparate in their height (e.g., see Fig. 2 above, where the 5° swathe from the pole is twice that of succeeding 5° latitudes.) This is a function of the projection being used within the octant, Cahill having three Variants: Equal-area, Conformal, and Gnomonic. (Only the truncated-octahedron Equal-area type is being considered here The other two use equilateral triangles, and so do not have polar incisions; but they cannot show an undivided polar area.)
In my re-working of Cahill, I wanted all adjacent geocells to be reasonably similar in size to each other. Not perfectly, of course; squashing a sphere demands compromise. Inner geocells of a Cahill-Keyes octant are smaller than outer ones. But the change is gradual, and no geocell is grossly out of whack with its neighbors. For me, this is an essential criterion, because I want the 1/1,000,000 Megamap not to have bloated geocells next to more normal ones. And I want the entire array of geocells closely resembling its globe-parent.
Therefore, the Cahill-Keyes design is sui generis. It does adapt Buckminster Fuller's Dymaxion map principle of having nominal globe scale along the outer edges of a facet, and shrinkage toward the middle. But in addition, unlike Fuller, or any other world map, its controlling desideratum is to keep neighboring geocells as similar as possible. (See "Photos of the Cahill-Keyes Megamap Prototypes", esp. Figs. 3, 6, and 7.) Consequently, its inner projection matches none of Cahill's three Variants.
("Projection" is not quite the right term here; "transformation" is closer.) Perhaps we could dub mine the "Proportional Geocell" or "Global Cognate" world map design.
None of Cahill's maps (nor Waterman) show concentric circles in the polar vertexes of the octants, but flattened arcs instead. When the right-angle polar zones of four octants are joined, the result is more like a rounded square, giving Antarctica a peculiar skeleton not resembling the rest of the map.6) Re-assemble Antarctica.
In my rendition of Cahill, I drew the first 16 parallels from the pole as circles (i.e., 17° including the pole itself): enough to include most of Antarctica, as if an orthographic, before the parallels gradually flatten as they approach the equator. A related question of polar design is the following:
This is a cue from Buckminster Fuller, whose otherwise questionable Dymaxion map includes a complete Antarctica as an integral part. Cahill's Butterfly never showed Antarctica entire: only its four pieces at the four southern vertexes. Moreover, the early versions had curved vertexes, which would not enable a contiguous polar reunion. It was only with the unpublished 1936 Equal Area "C" version that Cahill devised right angle vertexes, but even then he did not incorporate the frozen continent. (See entire map at this link, Fig. 9.2.1.)In sum, those were my major, outer, revisions of the Cahill design, relatively easy to describe. However, the inner distribution of parallels and meridians, what Cahill called the "intensive mathematical details" is another story. And I am no mathematician.
My approach is to duplicate three polar segments, 90° to 60° S each, and attach them to the remaining one beneath South America. The esthetic consideration is to have a single unified world map with all continents whole, and in place, and with continuity, rather than relegating Antarctica to be a separate stepchild.
The fine points of all that require a more detailed description. Suffice to say here that in October 1975 I drafted a preliminary Cahill-Keyes wall map, with a five-degree graticule, 1/20,000,000, in just a single week. However, when the parallels crossed from one octant to the next, they either sagged, or cusped upward. Back to the drawing board for several more years, to produce a much more refined octant template, with a one-degree graticule, establishing and executing the principle of "proportional geocells".
My third draft map was a 1/20,000,000 wall version, 1 x 2 meters, with one degree geocells, plus national and some provincial boundaries, but no rivers or other topography as yet. After that came computation tables for a more precise rendering at 1/10,000,000, and then for the 1/1,000,000 Megamap. (See "Photos of the Cahill-Keyes Megamap Prototypes".)
This is where things stood in 1984 when the project went into abeyance.
~ ~ ~
Explanatory Afterword, copied from the Megamap photos page:From 1975 to 1984 I did much preliminary calculation and design work toward a Cahill-Keyes 1/1,000,000 Megamap. I also executed by hand numerous drafts and prototypes.
Due to personal exigencies, the project was mothballed in 1984. Now that I am retired, and have a website, a 1998 Mac, and an HP scanner, I've begun to salvage some of that material — part of my effort to publicize the world map designs of B.J.S Cahill (1866-1944), the progenitor of my own mapwork.
As I mentioned elsewhere, my "Coherent World Map System" concept may be moot, but I think these notes and pictures warrant some space on the Web, rather than just languishing in my files.
Closely related to this page are the following papers of mine, already linked in the text body above.:
"Ten Principles for a Coherent World Map System"
"Geocells and the Megamap"
"Photos of the Cahill-Keyes Megamap Prototypes"
"Notes on Scaling Cahill and Cahill-Keyes Maps"
"Evolution of the Dymaxion Map: An Illustrated History and Critique"
(and see especially Part 9.2, "Total Irregularity of [its] Graticule"
Tags: B.J.S. Cahill, Cahill-Keyes, Megamap, cartography, Coherent World Map System, geocells, graticule, world map, Butterfly Map, "Real-World Map", 1/1,000,000, 1/10,000,000, 1/20,000,000, Buckminster Fuller, world map design