Cahill 1909
Cahill-Keyes 1975

Cahill 1909
|
Go back to
Gene Keyes home page
Cahill-Keyes 1975 |
|
Why Cahill? What about Buckminster Fuller?
Evolution of the Dymaxion Map: An Illustrated Tour and Critique Part 9.2 by Gene Keyes 2009-06-15 Summary: I
love Bucky, but Cahill's map is a lot better.
Here's how.
CONTENTS Click inside boxes to open other sections in separate windows. 9) Critique: Seven Design Flaws of Fuller's Map as Compared to Cahill's |
|
Part 9.2
Total Irregularity of Graticule In order to appreciate how badly disjointed the
Dymaxion map's graticule is, we first consider the total
graticular regularity of the Cahill octahedral — notwithstanding
my major criticism of Cahill's map, that its prime meridianal
division at 22 1/2º W, results in too many half degrees throughout.
(This was the main reason why I developed the Cahill-Keyes version,
divided at 20º W. As well, Steve Watermann
independently made the same decision.) In Fig. 9.1.1
on the previous page, the half-degrees are not apparent, because
the geocells are 7 1/2º. Nevertheless, all of Cahill's maps have
smooth and identical graticules in each octant. Although the half-degree
drawback is visible in the illustrations below, their graticular
regularity, symmetry, and identicality is manifest.
|
|
Fig. 9.2.1 below: In 1936, near the
end of his life, Cahill drafted a "penultimate" version of
Equal Area Variant, "C". But it went unpublished. I am debuting
it below, reduced to 1/100,000,000, one-quarter the size of an original
that was 1/25,000,000. Unlike his earliest Butterfly versions of
1909 et seq, this was executed with a 5º graticule (except
2 1/2º x 5º at the edges). Notice not only the graticular
identicality, but the smooth and regular curves throughout:
|
|
For a smaller picture size, click in it
once; to restore full size, click in it twice.
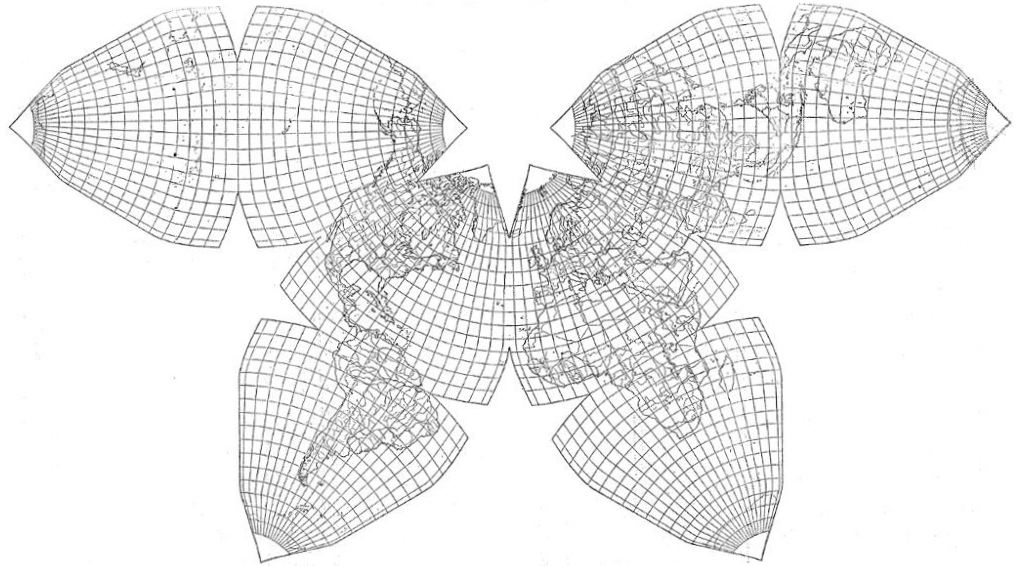
Source: Cahill archives, Bancroft Library, item #57, University of California, Berkeley. Hand-spliced from separate Xeroxes and digitally retouched by Gene Keyes. |
|
Fig. 9.2.2 below: Next, consider a Dymaxion
icosahedral map at 1/100 million. Because most Dymaxion
maps degrade their graticule to 15º, we cannot see very
well how they stack up against the neat array of 5º cells
in the Cahill above. (But keep reading...) Meanwhile, the helter-skelter
displacement of meridians and parallels is nonetheless evident, and
differently scattered in each facet:
|
|
For a smaller picture size, click in it
once; to restore full size, click in it twice.

Source: Dymaxion Map as drawn by Eric Gaba, Wikimedia Commons http://en.wikipedia.org/wiki/File%3AFuller_projection.svg (svg file converted to jpeg by Gene Keyes, and reduced on my monitor to 1/100,000,000 and triangle edges of 70.5 mm, from its original scale of 1/80,000,000). |
|
Fig. 9.2.3 below: Next we examine closer-up
the same area as shown by Cahill, and then Fuller: namely,
East Asia, Korea, and Japan, at 1/10,000,000, a scale 10 times
larger than Figs. 9.2.1 and 9.2.2 above (or click
to see them half-size at 1/20,000,000). (I have rotated both maps
"right side up" for comparison, even though I concur with Fuller et
al that there is no such thing as right side up, only habit. And convenience
of lettering direction.)
|
|
For a smaller picture size, click in it
once; to restore full size, click in it twice.

Source: Cahill archives, Bancroft Library, item #57, University of California, Berkeley. Hand-spliced from separate Xeroxes and digitally retouched by Gene Keyes and enlarged to 250% of original's scale of 1/25,000,000. |
|
Fig. 9.2.4 and 9.2.5 below: Now we reconsider
the Grip-Kitrick edition of the Dymaxion Map and its half-degree
graticule. With its anonymous latitude and longitude, the
overly-fine mesh seems quite innocuous. But in Fig. 9.2.5,
I have superimposed and identified a 5º graticule, as well
as some 1º geocells. As will be seen, this indicates how
badly a Dymaxion map disrupts the graticule. In these examples,
I have enlarged the scale (on my monitor) from 1/21,000,000 to 1/10,000,000
(or click to see it smaller at 1/20,000,000). Source note
for both items: see under Fig 9.2.5.
First, Fig. 9.2.4 below: |
|
For a smaller picture size, click in it
once; to restore full size, click in it twice.
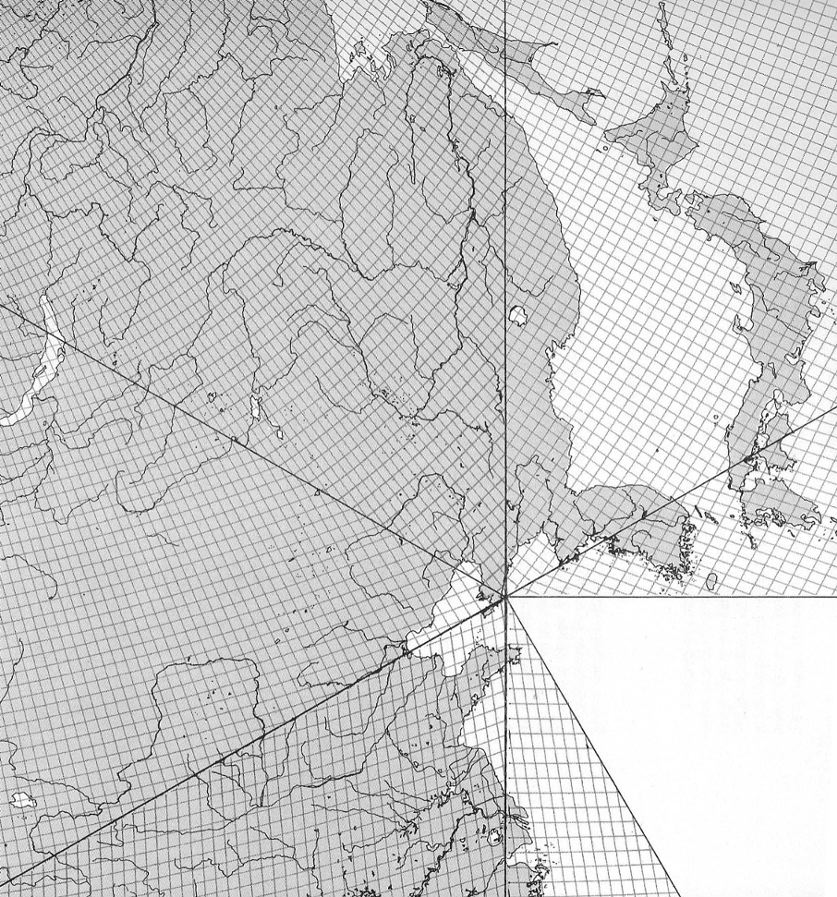
|
|
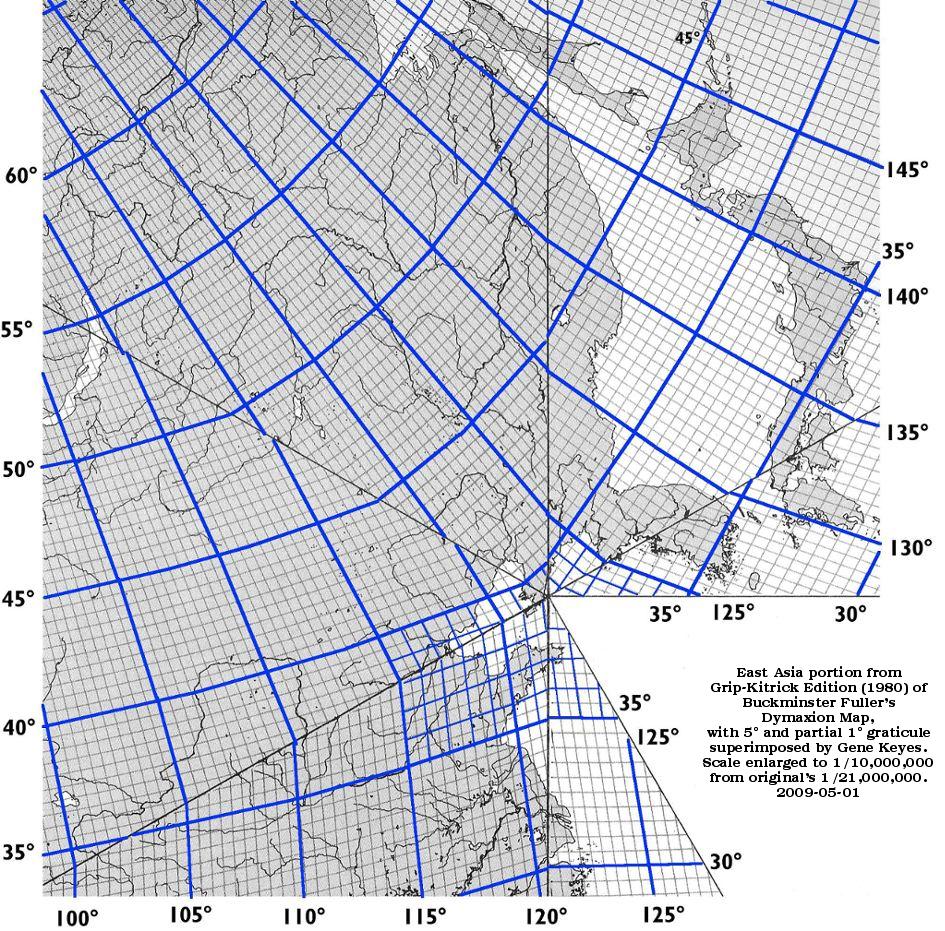
Fig. 9.2.5 below: And here is how any map
should truthfully portray its graticule, if we are to make
a judgment regarding its fidelity to a globe at the same scale
(line boldness is exaggerated for emphasis here; not that a map would
actually be done in this manner; but a 5º and 1º grid would
be plainly discernable):
|
|
For a smaller picture size, click in it
once; to restore full size, click in it twice.
|
|
Now we can appreciate the dreadful gash in the
5 x 5º geocell set comprising 120 - 125º E and
35 - 40º N. It is this same rip which tears Korea upward by 60º
from the Asian mainland, giving it an east-west orientation, rather
than north-south
Also apparent is the fact that along the triangle edges, the meridians and parallels do not have good continuity. Fuller states in his book Synergetics [Vol. 1], p. 701, that his "transformational projection model demonstrates how the mosaic tiles ... [go from curved to flat surface] without interborder crossing deformation of the mapping data." Maybe in principle; but at least in the very precise Grip-Kitrick rendition, this is not so. It is one more disadvantage of having a different graticule in every single facet, instead of Cahill's identical graticule in all octants. Source of Figs. 9.2.4 and 9.2.5:
Dymaxion Sky-Ocean World,
Grip-Kitrick Edition of Fuller Projection © 1980 by Buckminster Fuller excerpt scanned by Gene Keyes from personal copy, and adjusted (at least on my monitor*) from its actual triangle-edge length of 335 mm.and original scale, 1/20,700,000 to a triangle edge length of 352 mm, for a scale of 1/20,000,000. In Fig. 9.2.5: 5º and partial 1º graticule and numbering superimposed by Gene Keyes *Distance between vertex and west coast of Japan should be 95 mm; otherwise, adjust your settings or do the math (as explained here). |
|
Fig. 9.2.6 below: We are not finished.
Now consider the Cahill map with numbering added to the meridians and
parallels; and compare their smooth continuity, to the Fuller map's
breaks, bends, and disruptions: Notice above, for instance, the ordeal
of 125º E, or the "unparalleled" northward swing of the 40th parallel,
which, of course, should be heading due east; then recheck those same
lines below in Cahill:
|
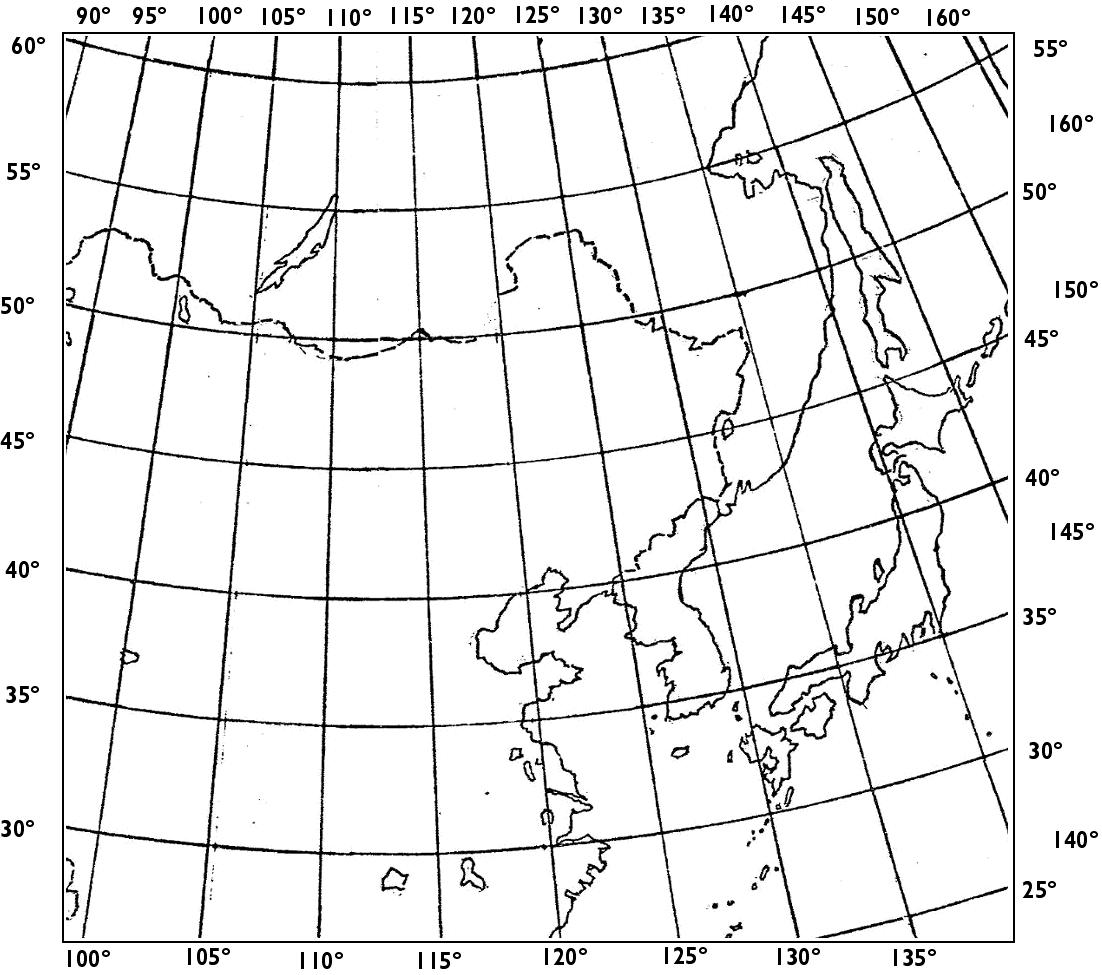
Source: Cahill archives, Bancroft Library, item #57, University of California, Berkeley. Hand-spliced from separate Xeroxes and digitally retouched by Gene Keyes Enlarged to 250% of original's scale of 1/25,000,000, with numbering added by GK. |
|
Let me now reprise in smaller compass how East
Asia should look on a world map of good fidelity to
a globe: taking Cahill as the gold standard. These segments are
reduced to 1/50,000,000. The important thing is that both
have a 5º graticule, and that is what enables tell-tale
comparison to a globe of 5º: Let us say: a ten-inch 1/50,000,000
globe.. Due to the lack of such globes (except FDR's), I am showing
a computer-drawn 10-inch orthographic (globe-like) map (Fig. 9.2.7),
and then a photo of my own 10-inch globe, onto which I improvisationally
pencilled 5º geocells, and marked with Cahill-Keyes octants (Fig.
9.2.8):
|
|
Fig. 9.2.5-b: Grip-Kitrick 1980
Dymaxion Map, with 5º geocells superimposed by Gene Keyes:
|
Fig.
9.2.6-b: Cahill's 1936 Equal Area Variant "C", numbering added
by Gene Keyes. |

|

|
|
Fig. 9.2.7 and 9.2.8 below: Cahill
(Fig. 9.2.6-b above) comports well with a globe.
Fuller (Fig. 9.2.5-b above) does not: (More images of this Cahillized map and globe combo in Part 9.7-b.) 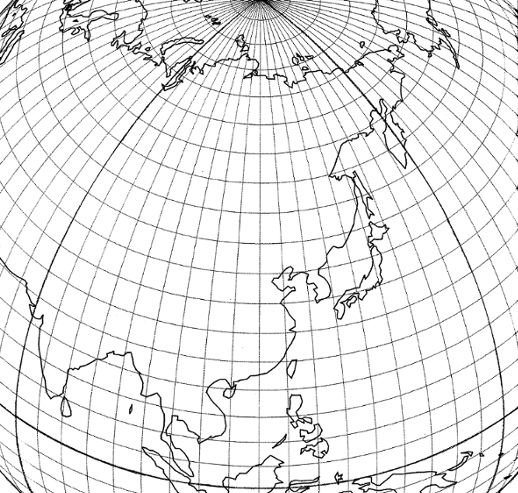
Source: Orthographic projection from R.L. Parker's "Supermap" program, output in 1975, and octants added, by Gene Keyes |
|
Fig. 9.2.8 below: Picture
of a 10-inch globe with the same 1/50,000,000 scale as above.
(More about this globe in Parts 9.6, and 9.7-b.)
|

Source: 1975 Replogle globe, with 5º geocells
added by Gene Keyes 2009;
photo by GK |
|
Having shown how badly ruptured the graticule is
in the East Asia area, I next extend my remarks about how the Dymaxion map
contorts not only Korea, but also Norway.
|