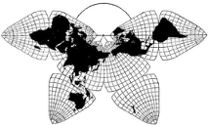
Cahill 1909
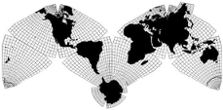
Cahill-Keyes 1975

Cahill 1909
|
Go back to
Gene Keyes home page
Cahill-Keyes 1975 |
|
Why Cahill? What about Buckminster Fuller?
Evolution of the Dymaxion Map: An Illustrated Tour and Critique Part 9.5 by Gene Keyes 2009-06-15 CONTENTS
Click inside boxes to open other sections in separate windows. 9) Critique: Seven Design Flaws of Fuller's
Map as Compared to Cahill's
|
|
Part 9.5
Anti-metric measurements I have already broached this problem in Part 8. Suffice to reprise here that Fuller's icosahedral not only snubs the metric system, but would do a poor job even if it tried to use it. The controlling true-scale icosahedral triangle edges have an unstated and irrational metric length of 7,048.89 km. Fuller, the old sailor, only gives distance in nautical miles, and those too have an irrational per edge distance of 3,806. It is ironic that the patron of the whole-earth philosophy would shun the very measurement which itself derived from the whole-earth circumference, that 1/10,000th decimal portion of a quarter great circle, equator to pole. Those irrational bases of the icosahedral map in turn lead to haphazard and irrational scales (e.g., 1/43,520,000) that do not neatly tie into metric lengths, as does 1/20,000,000 (to which I re-adjusted various examples in this set). Other Fuller maps have a medley of sui-generis scales such as 1/21,000,000, and 1/47,500,000 and 1/77,500,000, etc., and that's not including the second "shrunken" scale where mentioned. The Fuller map therefore, unlike Cahill, has no chance to combine three fundamentals: of whole-earth elementary education: 1) a synoptic globe-plus-map pairing;A Cahill map (and readily made cognate globe) would enable just such a three-fold teaching of geographic fundamentals: • its obvious map-globe relation; |
|
The anti-metric nature of the Dymaxion map in
turn is symptomatic of its overall lack of fidelity to a globe, as elaborated
next.
|