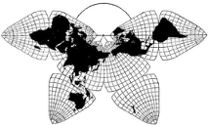
Cahill 1909
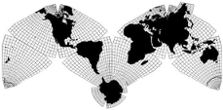
Cahill-Keyes 1975

Cahill 1909
|
Go back to
Gene Keyes home page
Cahill-Keyes 1975 |
|
Why Cahill? What about Buckminster Fuller?
Evolution of the Dymaxion Map: An Illustrated Tour and Critique Part 9.7-a by Gene Keyes 2009-06-15 CONTENTS
Click inside boxes to open other sections in separate windows. 9) Critique: Seven Design Flaws of Fuller's
Map as Compared to Cahill's
|
|
Part 9.7-a
Learnability: synoptic view, globe and map Thirty-six years ago in 1973-74,
when I was still enamored of Fuller's icosahedral, and using
it as the base map in my MA thesis, I tried my utmost to make
the disparate pieces learnable and identifiable as global components.
I assigned numbers to each triangle, starting at Antarctica, and
spiraling to the North Pole. I assigned matching-pair numbers
to each vertex, and matching-pair numbers to each triangle side.
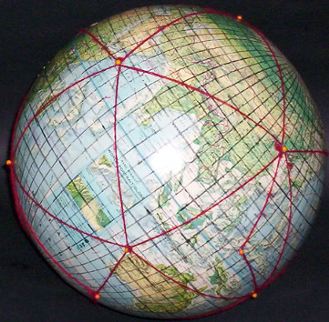
I drew a five-degree graticule on a 12-inch globe — what an exercise
that was — , pushed in map pins at the vertex points, and strung
red yarn into a spherical icosahedron, including the dubious split
pieces. (All shown in Appendix 1 below.)
That whole endeavor, like Fuller's icosahedral map, was the very opposite of "keep it simple"; the opposite of Occam's Razor, that 'entities are not multiplied unnecessarily'; the opposite of Einstein's dictum to 'Make everything as simple as possible, but not simpler.' If only I had known beforehand of the Cahill map's far greater elegance. The vivid superiority of the Cahill design is manifest when it comes to comparing an octahedral map to a globe. The similarity is obvious and easy to grasp. With Cahill's three cuts, the globe is divided into eight easy pieces: • Each piece has an equatorial base and a polar vertex.A Cahill map is therefore not only a thing of beauty, but a teaching tool of unmatched simplicity and finitely-visible entirety. A Fuller map is a thing of excessive complexity and perplexity; asymmetry and unlearnability: • Most pieces lack either a pole or portion of Equator. And as I stress over and over again, a Cahill world map had all the continents undivided and relatively undistorted, long before Fuller reinvented that wheel, in a much klutzier design. (Fuller's derivative geodesic dome is a thing of beauty, but the principle is not suitable for a map. Fuller's whole-earth narratives, and World Game, are also a joy to behold, but can be done on a Cahill map.) Because my criticisms overlap and interlink, especially in regard to learnability, let me restate an argument I made in Part 9.5 about the anti-metric aspect: Fuller's map fails both to provide and to combine three fundamentals of whole-earth elementary education: 1) a synoptic globe-plus-map pairing;Of course, it also fails to provide a fourth fundamental of map learning: national boundaries (though this is not a function of Fuller's projection, only his predilection). I heartily agree that humanity needs to outgrow chauvinism and nationalism, but boundaries cannot be wished away, any more than a medical book can decline to discuss cancer. Temperature zones and remote image composites are all to the good, but are only single layers of a multiplex global mosaic. Fuller, however, tended to be so possessive of his patents and copyrights that he sometimes stifled development of his ideas, including the Dymaxion map. His failure to provide one-and-five-degree resolution is not Fuller's alone; most single world maps and globes suffer from that shortcoming. But Fuller in his later versions had watered down his 1943 map's 5° graticule, to the faint 15° which would not so obviously reveal their mis-shapes. Cahill, on the other hand, had started with sub-standard 7 1/2° or 15° graticules, but by 1936 had graduated to 5° geocells: too late in his life, sadly, for these to be published. (Except above in Part 9.2, for the first time anywhere, and repeated one octant at a time in Part 9.7-b.) Fuller emphasizes the closed-system nature of his map, an important criterion, unlike most other commonplace open-ended world maps — except Cahill, who also links all facets of the globe to one another in various possibilities. But in my own learning experience, from grade school to grad school, I also found any globe itself to be confusingly open-ended — until I absorbed the Cahill map + globe into my mindset: those eight equal pieces, flat or spherical. It occurs to me that a globe without a Cahill-octahedral division is like a fat book without chapters; and that a globe / world map without a five-degree grid is like a long chapter without paragraphs. The learnability of the Cahill world map is its near-identity with a globe so-marked into eight comprehensible symmetrical octants. The unlearnability of the Fuller map is its 22 facets, mismatched to a globe's meridians and parallels; not only asymmetrical as a whole, but asymmetrical and irregular within every single piece. |
|
Appendix 1
The clumsy relation of Fuller's icosa-triangles to a globe As emphasized above — and shown on the following
page in Appendix 2 —, a Cahill octahedral has eight easy-to-grasp
octants, each with a distinct content of land-mass and water. Each octant
is easy to remember in its own right. The whole set in effect goes
around the globe twice: once to show the northern hemisphere in four
pieces, once for the southern, in four pieces. (Or, centered on the
dividing meridian, the whole set of on-globe octants can be seen, two
at a time, in four frames, rather than eight.) Orientation is easy to
maintain, whether one takes a polar, equatorial, or temperate zone viewpoint.
Each octant goes from pole to equator; each is unmistakable, by itself,
or seen with a globe.
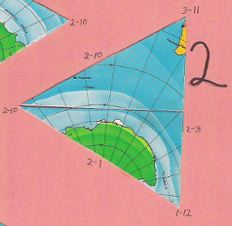
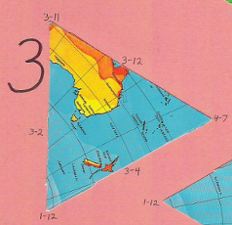
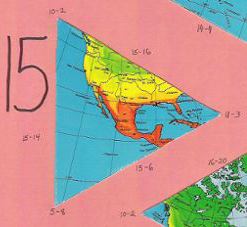
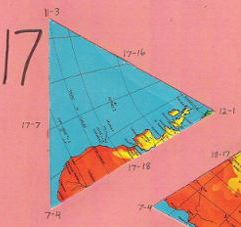
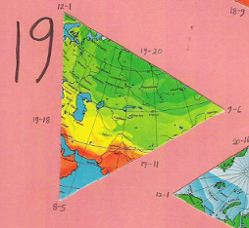
But with a Fuller icosahedral, one quickly becomes lost among the disparate, disjointed, disorienting set of 20 (or 22) triangles-plus-polygon. Four of them are all-ocean, and nearly indistinuishable from one another. Only eight have segments of the equator. Only four have parts of the poles. Notice also, for instance, how Fuller's South America is divided over four different facets, whereas Cahill's South America is in two. Fuller's Australia straddles three facets; Cahill gets it all in one. It is a puzzle, in the derogatory sense of the word. (One can assemble a Dymaxion map puzzle from its 22 pieces on the Internet, but that is only an amusement, not a learning experience as is, for example, a jigsaw map of separate U.S. states — or the Cahill octants themselves.) Ironically, the fragmented components of a Dymaxion map are just the opposite of Fuller's whole-earth purview. |
|
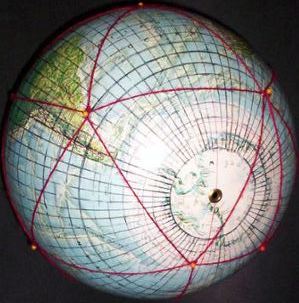
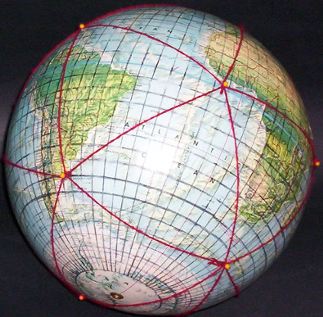
In the photos below, I have re-scaled a 12-inch
globe to appear as if five inches, and a scale of 1/100,000,000.
(Which happens to be ten times smaller than President Roosevelt's fifty-inch,
5º globe of 1/10,000,000.) The measurements are approximate, given
the variables of perspective, and digital reprocessing, and how they
appear on my monitor. However, it is done like this:
As shown in Part 8, "Notes on Scaling Dymaxion Maps", the [unstated] edge length of a Fuller triangle is 7,048.89 km. Thus, on a 1/100,000,000 globe, the edge length is 70.5 mm. I adjusted the pictures to depict (on average) a distance of 70.5 mm between the center of pin-heads (selected, depending on perspective). Likewise reduced are the edge lengths of the counterpart flat triangles, from 91 mm down to 70.5 mm. These are reprinted from my 1973 MA thesis, at 1/100,000,000, not their original scale of 1/77,500,000. As mentioned, I had numbered each facet as well as its edges and vertices, spiraling from South Pole to North Pole. Source for all images in this series: Rand McNally 12 inch globe;
5° grid and icosa triangles superimposed by Gene Keyes, 1974; photos by GK, 2009 Facets from [1967] Honeywell foldup globe (see Part
6, Fig. 6.1)
R. Buckminster Fuller and Shoji Sadao, Cartographers © 1954, 1967 by Buckminster Fuller Cut and numbered by Gene Keyes, 1973; scanned by GK, 2009. |
|
|

|
|

|
|

|
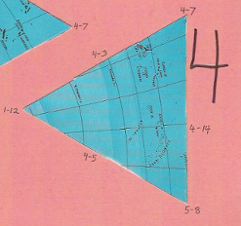
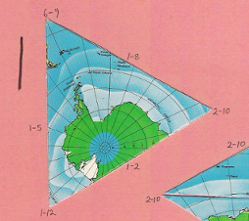
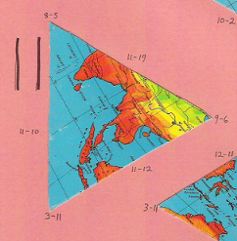
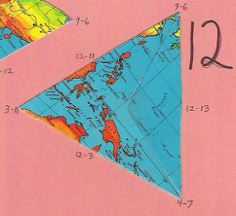
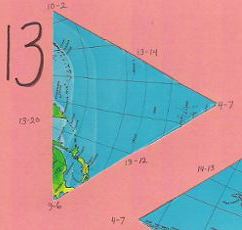
One of four almost indistinguishable ocean pieces |

|
|

|
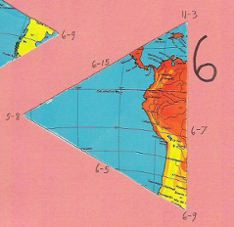
|

|

|
|

Second of four almost indistinguishable ocean pieces |

|
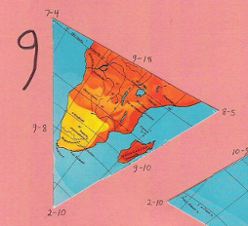
|

|
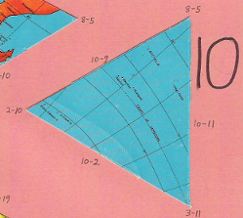
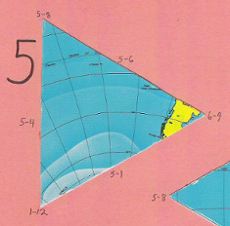
Third of four almost indistinguishable ocean pieces |
|
|

|
|

|
|

|
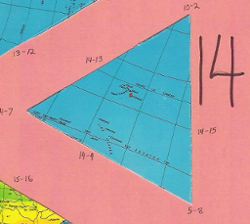
Fourth of four almost indistinguishable ocean pieces |

|
|

|

|

|
|

|

|

|
|

|
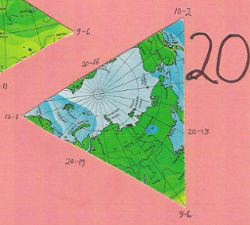
|
|
Because there are so many illustrations in Part
9.7, I am putting Appendix 2 on the next page. Like the Fullerized
globe above, the following is an image set of a 5° Cahillized globe and its
flat octant counterparts.
Go to Part 9.7-b, Appendix 2
Learnability: synoptic view, globe and map (continued) Appendix 2 The close relation of Cahill's octants to a globe |