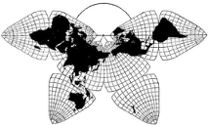
Cahill 1909
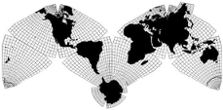
Cahill-Keyes 1975

Cahill 1909
|
Go back to
Gene Keyes home page
Cahill-Keyes 1975 |
|
Why Cahill? What about Buckminster Fuller?
Evolution of the Dymaxion Map: An Illustrated Tour and Critique Part 9.4 by Gene Keyes 2009-06-15 CONTENTS
Click inside boxes to open other sections in separate windows. 9) Critique: Seven Design Flaws of Fuller's
Map as Compared to Cahill's
|
|
Part 9.4
Poor scalability As Korea and Norway illustrate, the larger a Dymaxion map, the worse it looks, provided it has a complete 5º or 1º graticule; otherwise it gets away with artistic license. By contrast, a Cahill map and graticule is good at any scale from smallest to largest, whole continents and all. The underlying premise and precept of my critique of Fuller, and advocacy of Cahill, is that there be a single general-purpose world map which can be used at the very smallest to the very largest scales, while bearing good fidelity to a globe at any size. This is why I stress the importance of a regular 5º or 1º graticule. The more irregular a world map’s graticule, the worse and worse it looks as the scale is magnified. This is the fate of Fuller’s map. With its perfunctory 15º graticule concealing the weakness of its underlying chassis, its king-size versions do not accurately match an atlas map, or equivalent globe at the same scale. As shown in Part 6, the World Game's first "Big Map" of 1/2,000,000 was not a Dymaxion map, but a patchwork of other projection-sheets which could not and did not match edge to edge; gaps were simply papered over. The subsequent "Earth Voyage" map, also at 1/2,000,000, has the old diluted 15º graticule, and is not a world map for close-up examination, but only a very simplified set decoration in colors redolent of grade-one geography books. To repeat: I’m not scoffing at either "Big Map" version; they do portray the whole-earth, sky-ocean vision of Bucky in a remarkable expanse. But they do not enable a continuum in the same layout of the whole earth as seen at the largest possible scales and details with the finest possible graticule of one degree, accentuated by five degrees. As shown earlier, the Grip-Kitrick half-degree resolution is just as misleading as the watered-down 15º versions because they do not relate to the real distribution of five-degree geocells on a globe. So when I say Fuller lacks scalabillity, I mean that its hodge-podge graticule does not stand up to scrutiny, the more so the larger its scale. The Dymaxion has a semblance of authenticity in its large editions, but only a semblance, due to its lack of an authentic graticule of high resolution. And if we take "scalability" in another sense of the term, I have already described in Part 8 the difficulty of ascertaining scales in various Dymaxion maps — until you twig to the unstated irrational 7,048.89 kilometer length of each triangle edge. That figure is a nuisance to work with, compared to the original-metric edge length of 10,000 km in octants a la Cahill. Fuller's anti-metric globe-math is almost as retrograde as Roman numerals. (Just as geodesic dome strut lengths require elaborate tables of many different irregular figures: OK for architects and engineers; not so good for teaching about a globe.) Likewise, his 20 vertex points are a finicky multi-digit set of degree-minute-second readings, divorced from any meridian or parallel. Cahill's six vertex points [as put on whole-number longitudes by both me, and Waterman] are simplicity itself: two poles, and four meridians on the equator, 90º apart. (first meridian, 20º W and 160º E; second meridian, 110º W, and 70º E; each pair being 180º ). Fuller's points are a different story, seen in the following charts. (Indeed, his very icosahedron is subject to some wobble as to just what its fixed orientation finally is, as we saw in the difference between the Raleigh or Honeywell versions, and the more accurate Grip-Kitrick, as well possibly others indicated in Fig. 9.4.2.) |
|
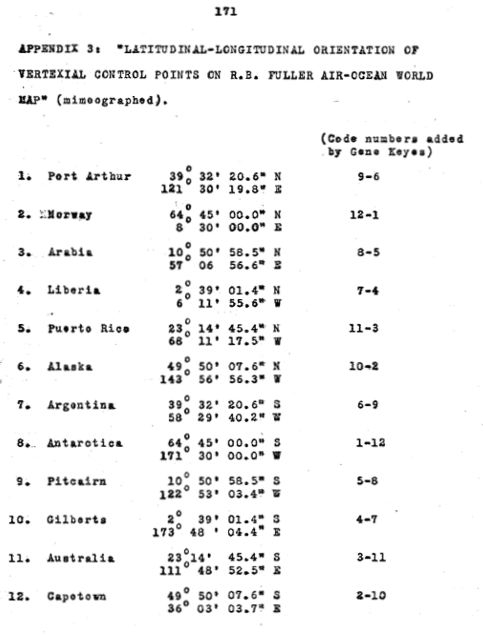
Fig. 9.4.1 below: Fuller's "Vertexial control
points", which I included on p. 171 of my 1973 M.A. thesis, as copied
from an undated, unsourced, mimeographed list I saw at Southern Illinois
University, Carbondale [either the SIU map library, or Fuller's then office
in Carbondale, the World Resources Inventory]. In this one, nos. 1 and
2 (Fuller's numbering) happen to be those two "weak points" of the map
which I cited in Part 9.3.
|
|
|
Fig. 9.4.2 below: A different list is online
at Robert W.
Gray's website, but I am also copying it all here for purposes of
comparison. Besides this one, Gray alludes to three other varying lists.
|
Source: http://www.rwgrayprojects.com/rbfnotes/maps/graymap4.html
* * *
|
|
[Gene Keyes again.] Next I make some remarks on
the educational implications of the Dymaxion map's anti-metric character.
|